I haven't yet found a Web tutorial detailing how to derive the formulas for Latent Dirichlet Allocation using a Mean-Field Variational approach, so I thought I could just as well write this blog about it.
Latent Dirichlet Allocation (LDA) is a common technique to determine the most likely topics that are latent in a collection of documents. Blei's (2003) seminal paper introduces LDA and explains a variational approach which is the reference of later work. All tutorials that I have found so far end up referring to Blei's paper, but for people like me, they do not give enough detail.
Wikipedia has a page that explains LDA and how to implement it using Gibbs sampling methods. There's another page in Wikipedia that explains Variational Bayesian methods of the sort that I'm going to cover here, but their examples (based on chapter 10 of the excellent book by Bishop) do not cover the case of LDA.
So, in this blog I will derive the formulas for the variational approach to LDA from scratch, by relying on the theory and examples explained in Bishop's book.
LDA models a document as being generated from a mixture of topics according to this generative model:
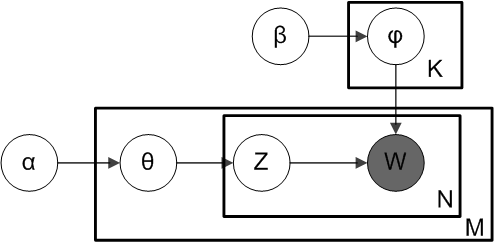
The generative process can be expressed with this plate diagram:
("Smoothed LDA" by Slxu. public - Own work. Licensed under CC BY-SA 3.0 via Wikimedia Common)
$$
P(W,Z,\theta,\varphi;\alpha,\beta) = \prod_{k=1}^KP(\varphi_k;\beta)\prod_{m=1}^MP(\theta_m;\alpha)\prod_{n=1}^NP(z_{mn}|\theta_m)P(w_{mn}|z_{mn},\varphi)
$$
If we substitute the probabilities by the respective formulas for the Multinomial and Dirichlet distributions, we obtain:Latent Dirichlet Allocation (LDA) is a common technique to determine the most likely topics that are latent in a collection of documents. Blei's (2003) seminal paper introduces LDA and explains a variational approach which is the reference of later work. All tutorials that I have found so far end up referring to Blei's paper, but for people like me, they do not give enough detail.
Wikipedia has a page that explains LDA and how to implement it using Gibbs sampling methods. There's another page in Wikipedia that explains Variational Bayesian methods of the sort that I'm going to cover here, but their examples (based on chapter 10 of the excellent book by Bishop) do not cover the case of LDA.
So, in this blog I will derive the formulas for the variational approach to LDA from scratch, by relying on the theory and examples explained in Bishop's book.
Generative Model
LDA models a document as being generated from a mixture of topics according to this generative model:
- For k = 1 .. $K$:
- $\varphi_k \sim \hbox{Dirichlet}_V(\beta)$
- For m = 1 .. $M$:
- $\theta_m \sim \hbox{Dirichlet}_K(\alpha)$
- For n = 1 .. $N_m$:
- $z_{mn} \sim \hbox{Multinomial}_K(\theta_m)$
- $w_{mn} \sim \hbox{Multinomial}_V(\sum_{i=1}^KZ_{mni}\varphi_i)$
The generative process can be expressed with this plate diagram:
("Smoothed LDA" by Slxu. public - Own work. Licensed under CC BY-SA 3.0 via Wikimedia Common)
Joint Probability
According to the plate diagram the joint probability is:$$
P(W,Z,\theta,\varphi;\alpha,\beta) = \prod_{k=1}^KP(\varphi_k;\beta)\prod_{m=1}^MP(\theta_m;\alpha)\prod_{n=1}^NP(z_{mn}|\theta_m)P(w_{mn}|z_{mn},\varphi)
$$
P(W,Z,\theta,\varphi;\alpha,\beta)= \prod_{k=1}^K(\frac{1}{B(\beta)}\prod_{v=1}^V\varphi_{kv}^{\beta-1}) \prod_{m=1}^M\left(\frac{1}{B(\alpha)}\prod_{k=1}^K\theta_{mk}^{\alpha-1}\prod_{n=1}^N(\prod_{k=1}^K\theta_{mk}^{z_{mnk}} \prod_{k=1}^K\prod_{v=1}^V\varphi_{kv}^{w_{mnv}z_{mnk}} )\right)
$$
Variational Inference
We want to determine the values of the latent variables $\varphi,\theta,Z$ that maximise the posterior probability $P(\theta,\varphi,Z|W;\alpha,\beta)$. According to Bishop, Chapter 10, we can approximate the posterior with a product that separates $z$ and $\theta,\varphi$:$$
P(\theta,\varphi,Z|W;\alpha,\beta) \approx q_1(Z)q_2(\theta,\varphi)
$$
Here $q_1$ and $q_2$ are families of functions, and we choose $q_1^*$ and $q_2^*$ that best approximate P by applying the formulas:
$$
\ln q_1^* (Z) = \mathbb{E}_{\theta\varphi}\left[\ln P(W,Z,\theta,\varphi;\alpha,\beta)\right] + const
$$
$$
\ln q_2^* (\theta,\varphi) = \mathbb{E}_{Z}\left[\ln P(W,Z,\theta,\varphi;\alpha,\beta)\right] + const
$$
The constants are not important since we can determine their exact values later. Also, since these formulas use logarithms, the calculations can be simplified as we will see below.
Factor with $Z$
Let's start with $q_1(Z)$:
$$\ln q_1^*(Z) = \mathbb{E}_{\theta\varphi}\left[\ln P(W,Z,\theta,\varphi;\alpha,\beta)\right] + const$$
$$ = \sum_{k=1}^K\left((\beta-1)\sum_{v=1}^V\mathbb{E}(\ln\varphi_{kv})\right) $$
$$+ \sum_{m=1}^M\left((\alpha-1)\sum_{k=1}^K\mathbb{E}(\ln\theta_{mk})+\sum_{n=1}^N\left(\sum_{k=1}^Kz_{mnk}\mathbb{E}(\ln\theta_{mk})+\sum_{k=1}^K\sum_{v=1}^Vz_{mnk}w_{mnv}\mathbb{E}(\ln\varphi_{kv})\right)\right)+const$$
In this expression, terms that do not contain the variable $z$ are constant and therefore can be absorbed by the general $const$, simplifying the expression:
$$=\sum_{m=1}^M\sum_{n=1}^N\left(\sum_{k=1}^Kz_{mnk}\mathbb{E}(\ln\theta_{mk})+\sum_{k=1}^K\sum_{v=1}^Vz_{mnk}w_{mnv}\mathbb{E}(\ln\varphi_{kv})\right)+const$$
$$=\sum_{m=1}^M\sum_{n=1}^N\sum_{k=1}^Kz_{mnk}\left(\mathbb{E}(\ln\theta_{mk})+\sum_{v=1}^Vw_{mnv}\mathbb{E}(\ln\varphi_{kv})\right)+const$$
$$=\sum_{m=1}^M\sum_{n=1}^N\sum_{k=1}^Kz_{mnk}\left(\mathbb{E}(\ln\theta_{mk})+\sum_{v=1}^Vw_{mnv}\mathbb{E}(\ln\varphi_{kv})\right)+const$$
We can observe that the expression can be reduced to a combination of probabilities from multinomial distributions, since $\ln\left(\hbox{Multinomial}_K(x|p)\right) = \sum_{i=1}^Kx_i\ln(p_i)+const$ and conclude that:
$$q_1^*(Z)\propto\prod_{m=1}^M\prod_{n=1}^N\hbox{Multinomial}_K\left(z_{mn}\middle|\exp\left(\mathbb{E}(\ln\theta_m)+\sum_{v=1}^Vw_{mnv}\mathbb{E}(\ln\varphi_{.v})\right)\right)$$
We can determine $\mathbb{E}(\ln\theta_m)$ and $\mathbb{E}(\ln\varphi_{.v})$ if we can solve $q_2(\theta,\varphi)$ (see below).
Factor with $\theta,\varphi$
$$\ln q_2^* (\theta,\varphi) = \mathbb{E}_{Z}\left[\ln P(W,Z,\theta,\varphi;\alpha,\beta)\right] + const$$
$$=\sum_{k=1}^K\left((\beta-1)\sum_{v=1}^V\ln\varphi_{kv}\right)
$$
$$+
\sum_{m=1}^M\left((\alpha-1)\sum_{k=1}^K\ln\theta_{mk}+\sum_{n=1}^N\left(\sum_{k=1}^K\mathbb{E}(z_{mnk})\ln\theta_{mk}+\sum_{k=1}^K\sum_{v=1}^V\mathbb{E}(z_{mnk})w_{mnv}\ln\varphi_{kv}\right)\right)+const$$
All terms contain $\theta$ or $\varphi$ so we cannot simplify this expression further. But we can split the sum of terms into a sum of probabilities of Dirichlet distributions, since $\ln(\hbox{Dirichlet}_K(x|\alpha))=\sum_{i=1}^K(\alpha_i-1)\ln(x_i) + const$:
$$=\left(\sum_{k=1}^K\left((\beta-1)\sum_{v=1}^V\ln\varphi_{kv}\right)+\sum_{m=1}^M\sum_{n=1}^N\sum_{k=1}^K\sum_{v=1}^V\mathbb{E}(z_{mnk})w_{mnv}\ln\varphi_{kv}\right)$$
$$+\left(\sum_{m=1}^M\left((\alpha-1)\sum_{k=1}^K\ln\theta_{mk}+\sum_{n=1}^N\sum_{k=1}^K\mathbb{E}(z_{mnk})\ln\theta_{mk}\right)\right) + const$$
$$= (1) + (2) + const$$
Note that $(1)$ groups all terms that use $\varphi$, and $(2)$ groups all terms that use $\theta$. This, in fact, means that $q_2(\theta,\varphi)=q_3(\theta)q_4(\varphi)$, which simplifies our calculations. So, let's complete the calculations:
Subfactor with $\varphi$
$$\ln q_4^*(\varphi) = $$
$$= \sum_{k=1}^K\left((\beta-1)\sum_{v=1}^V\ln\varphi_{kv}\right)+\sum_{m=1}^M\sum_{n=1}^N\sum_{k=1}^K\sum_{v=1}^V\mathbb{E}(z_{mnk})w_{mnv}\ln\varphi_{kv}+ const$$
$$= \sum_{k=1}^K\sum_{v=1}^V\left(\beta -1 +\sum_{m=1}^M\sum_{n=1}^N\mathbb{E}(z_{mnk})w_{mnv}\right)\ln\varphi_{kv} + const$$
Therefore: $q_{4}^*(\varphi) \propto \prod_{k=1}^K\hbox{Dirichlet}_V\left(\varphi_k\middle|\beta+\sum_{m=1}^M\sum_{n=1}^N\mathbb{E}(z_{mnk})w_{mn.}\right)$
Subfactor with $\theta$
Similarly, $\ln q_3^*(\theta) = $
$$\sum_{m=1}^M\left((\alpha-1)\sum_{k=1}^K\ln\theta_{mk}+\sum_{n=1}^N\sum_{k=1}^K\mathbb{E}(z_{mnk})\ln\theta_{mk}\right) + const$$
$$ = \sum_{m=1}^M\sum_{k=1}^K\left(\alpha-1 + \sum_{n=1}^N\mathbb{E}(z_{mnk})\right)\ln\theta_{mk} + const$$
Therefore: $q_{3}^*(\theta) \propto \prod_{m=1}^M\hbox{Dirichlet}_K\left(\theta_m\middle|\alpha+\sum_{n=1}^N\mathbb{E}(z_{mn.})\right)$
Algorithm
Now we can fit all pieces together. To compute $q_1^*(Z)$ we need to know $q_3^*(\theta)$ and $q_4^*(\varphi)$, but to compute these we need to know $q_1^*(Z)$. We know that $q_1^*(Z)$ follows a Multinomial distribution, and $q_3^*(\theta)$ and $q_4^*(\varphi)$ follow Dirichlet distributions, so we can use their parameters to determine the expectations that we need:
We are now in the position to specify an algorithm that, given some initial values of one of the parametres, it calculates the other, then it re-calculates the parametres alternatively until the values do not change beyond a threshold. The algorithm is:
- From the properties of Multinomial distributions we know that $\mathbb{E}(z_{mnk}) = p_{z_{mnk}}$, where $p_{z_{mnk}}$ is the Multinomial parameter. Therefore we can conclude that:
- $q_3^*(\theta) \propto \prod_{m=1}^M\hbox{Dirichlet}_K\left(\theta_m\middle|\alpha+\sum_{n=1}^Np_{z_{mn.}}\right)$
- $q_4^*(\varphi) \propto \prod_{k=1}^K\hbox{Dirichlet}_V\left(\varphi_k\middle|\beta+\sum_{m=1}^M\sum_{n=1}^Np_{z_{mnk}}w_{mn.}\right)$
- From the properties of Dirichlet distributions we know that $\mathbb{E}(\ln\theta_{mk}) = \psi(\alpha_{\theta_{mk}}) - \psi\left(\sum_{k'=1}^K\alpha_{\theta_{mk'}}\right)$, where $\alpha_{\theta_{mk}}$ is the Dirichlet parameter and $\psi(x)$ is the digamma function, which is typically available in standard libraries of statistical programming environments. Therefore we can conclude that:
- $q_1^*(Z) \propto \prod_{m=1}^M\prod_{n=1}^N\hbox{Multinomial}_K\left(z_{mn}\middle|\exp\left(\psi(\alpha_{\theta_{m.}}) - \psi\left(\sum_{k'=1}^K\alpha_{\theta_{mk'}}\right) + \sum_{v=1}^Vw_{mnv}\left(\psi(\beta_{\varphi_{.v}})-\psi\left(\sum_{k'=1}^K\beta_{\varphi_{k'v}}\right)\right)\right)\right)$
We are now in the position to specify an algorithm that, given some initial values of one of the parametres, it calculates the other, then it re-calculates the parametres alternatively until the values do not change beyond a threshold. The algorithm is:
- For m=1..M, n=1..N, k=1..K
- $p_{z_{mnk}}=1/K$
- Repeat
- For k=1..K, v=1..V
- $\beta_{\varphi_{kv}}=\beta+\sum_{m=1}^M\sum_{n=1}^Nw_{mnv}p_{z_{mnk}}$
- For m=1..M, k=1..K
- $\alpha_{\theta_{mk}}=\alpha+\sum_{n=1}^Np_{z_{mnk}}$
- For m=1..M, n=1..N, k=1..K
- $p_{z_{mnk}}=\exp\left(\psi(\alpha_{\theta_{mk}}) - \psi\left(\sum_{k'=1}^K\alpha_{\theta_{mk'}}\right) + \sum_{v=1}^Vw_{mnv}\left(\psi(\beta_{\varphi_{kv}})-\psi\left(\sum_{k'=1}^K\beta_{\varphi_{k'v}}\right)\right)\right)$
Note that step 2.1.1 means that $\beta_{\varphi_{kv}}$ is an update of $\beta$ with the expected number of times that word $v$ is assigned topic $k$. Likewise, step 2.2.1 means that $\alpha_{\theta_{mk}}$ is an update of $\alpha$ with the expected number of words in document $m$ that are assigned topic $k$. Finally, $p_{z_{mnk}}$ is the probability that a word in place $n$ of document $m$ is assigned topic $k$.
Some additional notes about this algorithm:
Some additional notes about this algorithm:
- The initialisation step just assigns $1/K$ to each element of $p_z$, but note that Bishop said that there are several local minima. Different initial states may lead to different results. So it may be worth to research the impact of initial values in the final result.
- There are several iterations over the entire vocabulary $V$, which may be computationally-expensive for large vocabularies. We can optimise this by noting that $w_{mn}$ is a vector of $V$ elements such that only one of them has a value of 1, and the rest is zero.
- Steps 1 and 2 inside the repeat cannot be done in parallel with step 3, but all steps inside these can be made in parallel, so this is an obvious place where we can use GPUs or CPU clusters.
Code
I implemented the algorithm in a Python program, but for some reason I do not get the expected results. I suspect that the step that derives $\theta$ and $\varphi$ from $\alpha_{\theta_{mk}}$, $\beta_{\varphi_{kv}}$ and $p_{z_{mnk}}$ is wrong, but there might be other mistakes.The code is in http://github.com/dmollaaliod/varlda
If you can find out what is wrong, please post a comment, or drop me a message.
2 comments:
What are the dot notations that appeared in the subscripts? I noticed that there are a couple of them, each appeared in different places (at the end of the subscript or at the beginning of the subscript). What do they mean?
Ok I get it. They are vectors with subscripts begin fixed... Thanks for the nice post man.
Post a Comment